3.9 Polygon Transformation

Polygon transformation involves applying translation, rotation, reflection, enlargement, and shear to polygons while preserving or modifying their properties.

Key Concepts:

• Translation:

  Moving every vertex of a polygon by a vector \(\begin{pmatrix} a \\ b \end{pmatrix}\). \[ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x + a \\ y + b \end{pmatrix} \]

• Rotation:

  Rotating a polygon by \(90^\circ\) counterclockwise about the origin transforms each vertex: \[ (x', y') = (-y, x). \]

• Reflection:

  Flipping a polygon across a given axis. \[ \text{Reflection over the y-axis: } (x, y) \to (-x, y). \] \[ \text{Reflection over the x-axis: } (x, y) \to (x, -y). \]

• Enlargement:

  Scaling a polygon by a factor \(k\) about the origin: \[ (x', y') = (kx, ky). \]

• Shear:

  Distorting a polygon along an axis while keeping one dimension fixed. \[ \text{Horizontal shear: } (x', y') = (x + ky, y). \]

Examples:

Example 1: Translating a Triangle

A triangle with vertices \(A(1,2)\), \(B(3,4)\), and \(C(5,1)\) is translated by the vector \(\begin{pmatrix} -2 \\ 3 \end{pmatrix}\). Find the new coordinates.

Solution:

Using the translation formula: \[ A'(1-2, 2+3) = (-1,5), \] \[ B'(3-2, 4+3) = (1,7), \] \[ C'(5-2, 1+3) = (3,4). \]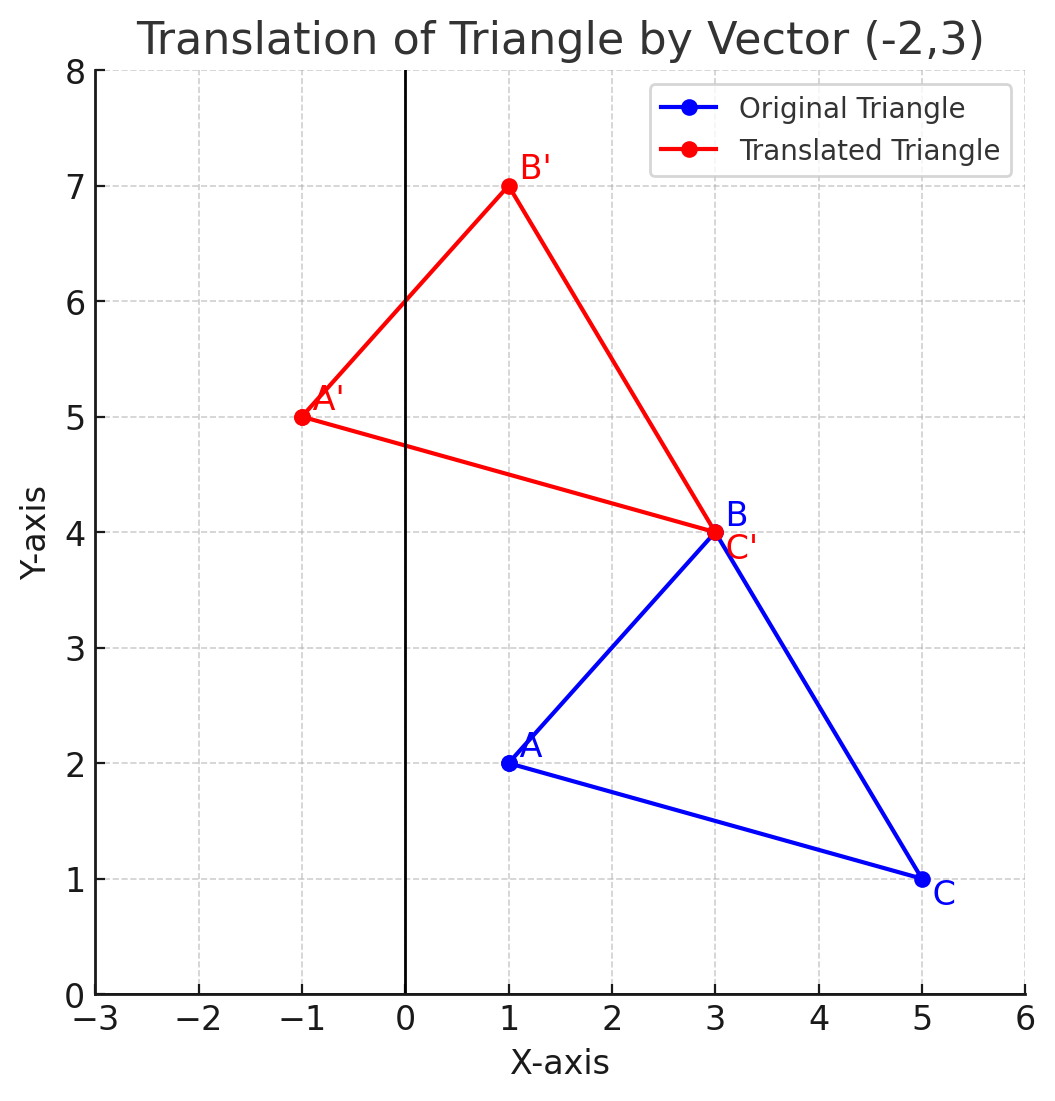 Thus, the translated triangle has vertices **\(A'(-1,5)\), \(B'(1,7)\), and \(C'(3,4)\)**.

Example 2: Rotating a Square by \(90^\circ\)

A square has vertices \(A(1,1)\), \(B(3,1)\), \(C(3,3)\), and \(D(1,3)\). Find the new coordinates after rotating it \(90^\circ\) counterclockwise about the origin.

Solution:

Using the rotation formula \((x', y') = (-y, x)\): \[ A'(1,1) \to (-1,1), \] \[ B'(3,1) \to (-1,3), \] \[ C'(3,3) \to (-3,3), \] \[ D'(1,3) \to (-3,1). \]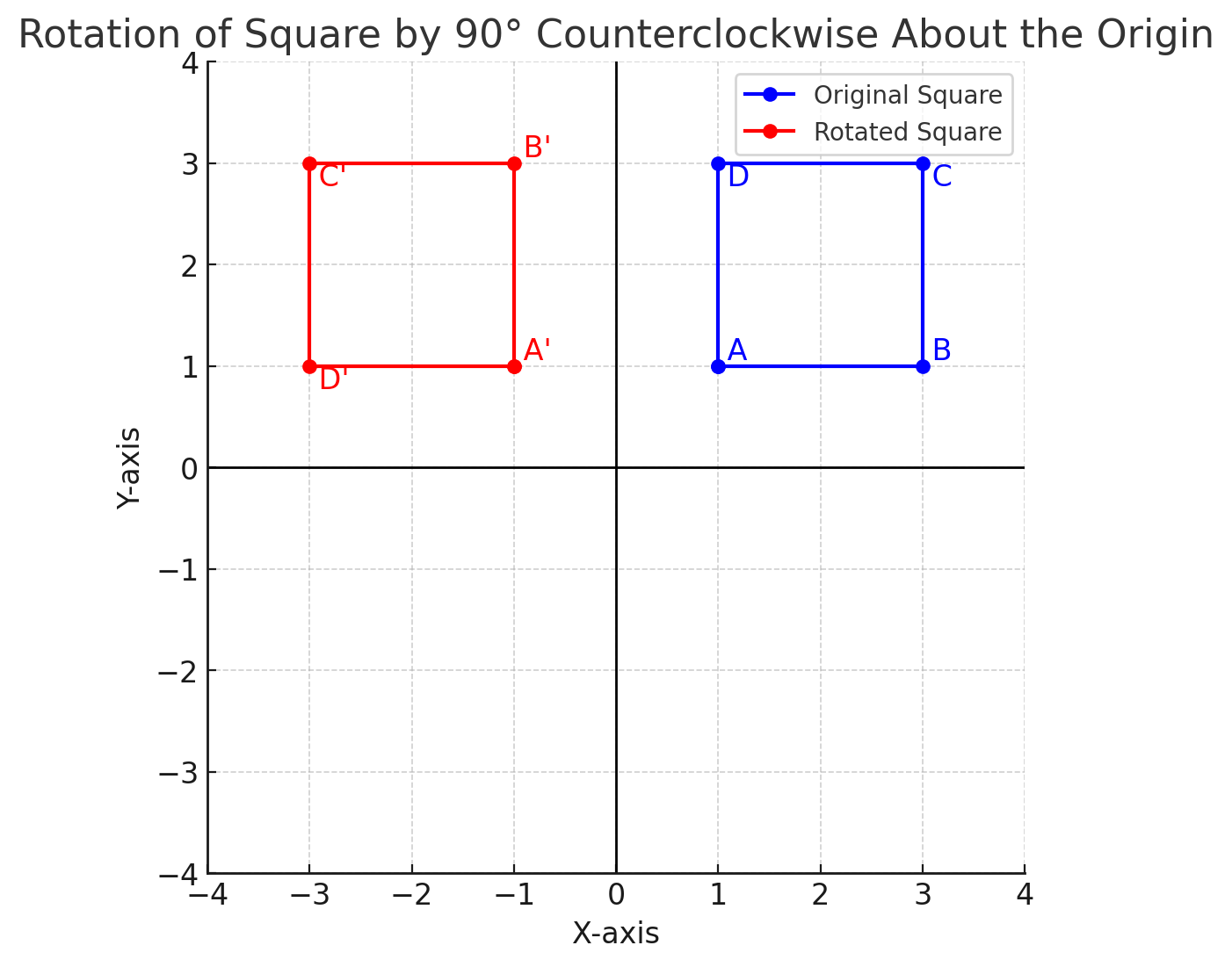 Thus, the rotated square has vertices **\(A'(-1,1)\), \(B'(-1,3)\), \(C'(-3,3)\), and \(D'(-3,1)\)**.

Example 3: Enlarging a Rectangle by Scale Factor 2

A rectangle has vertices \(A(1,2)\), \(B(4,2)\), \(C(4,5)\), and \(D(1,5)\). Find the new coordinates after enlarging it by a scale factor of 2 about the origin.

Solution:

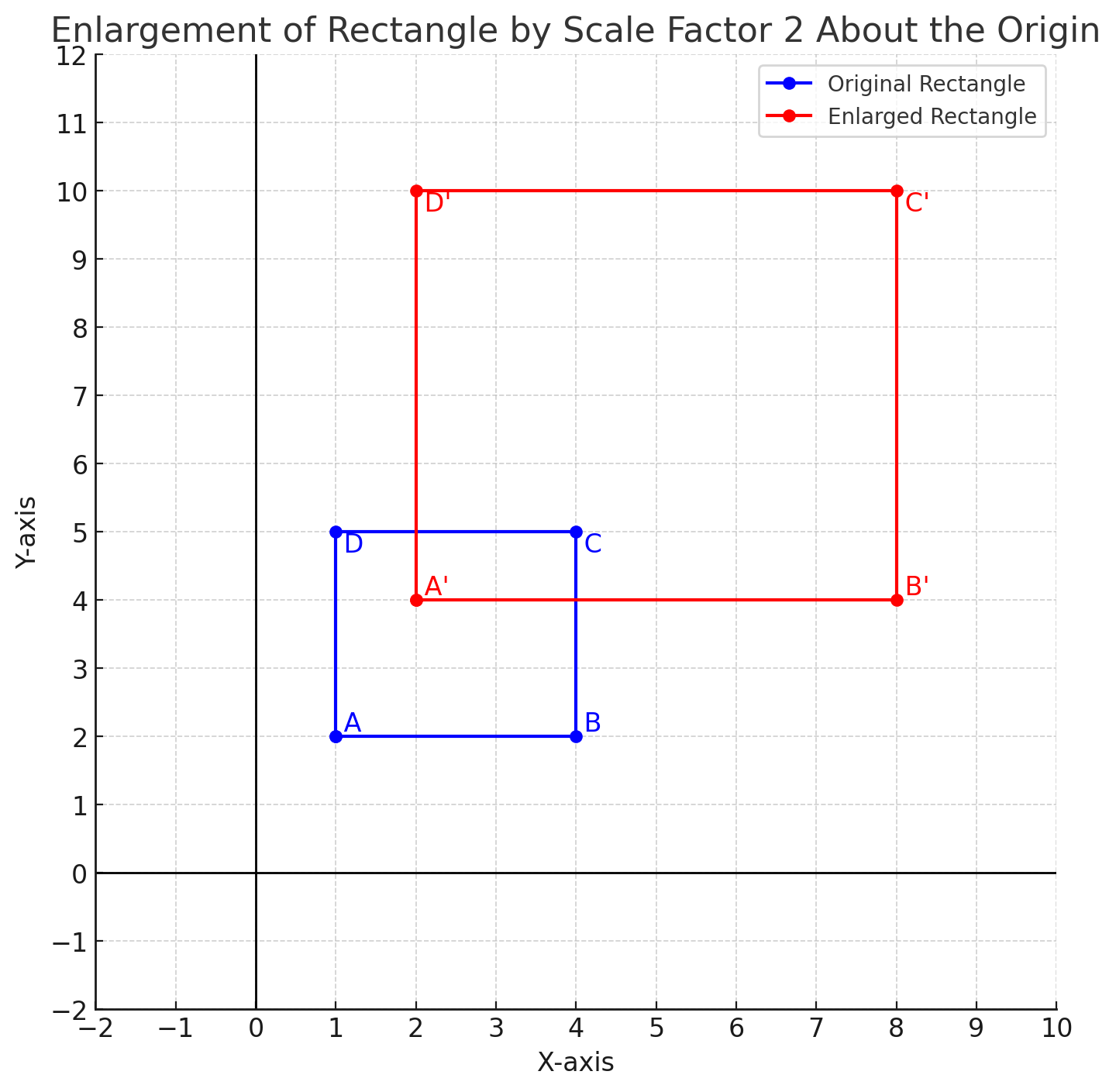
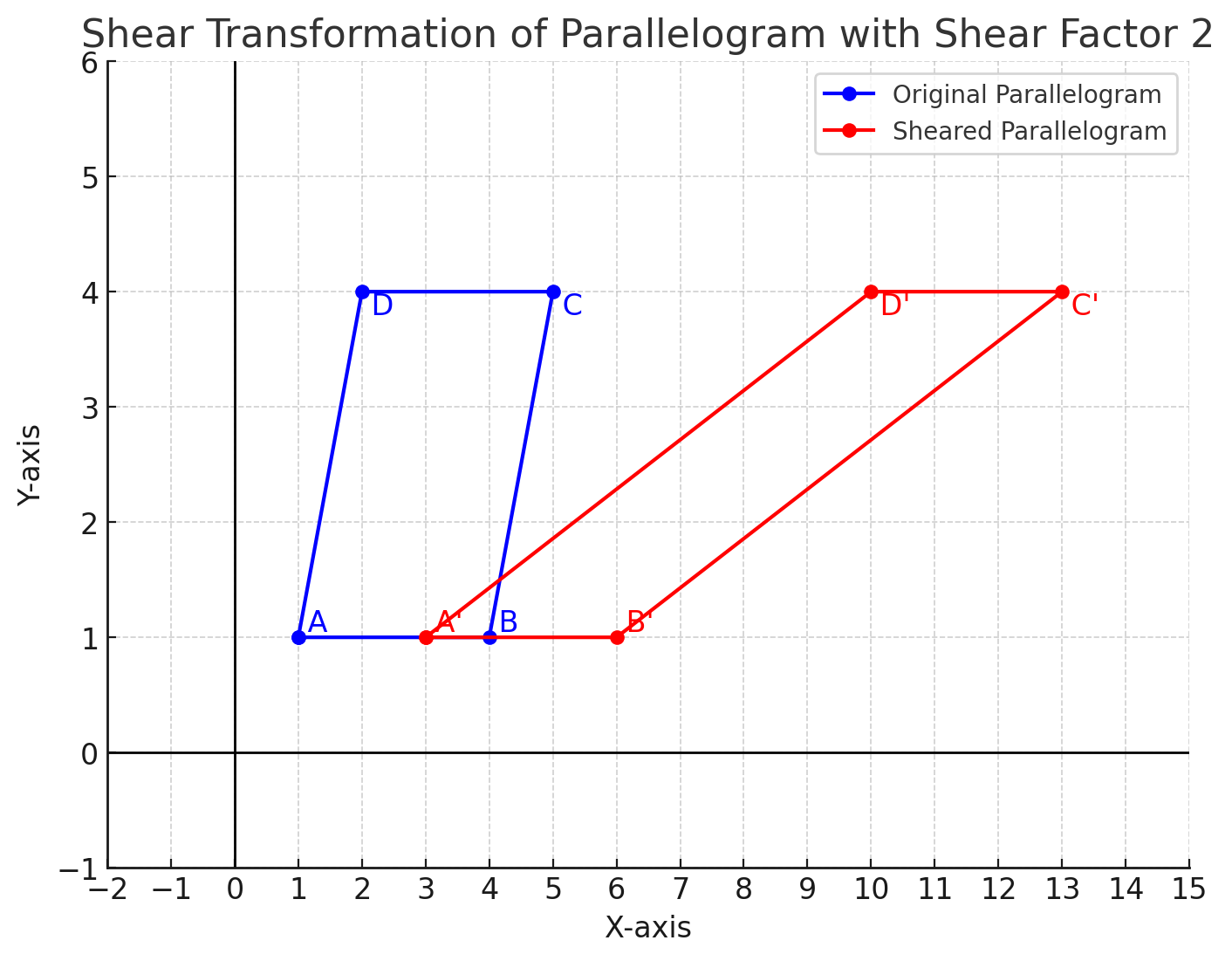
Using the enlargement formula \((x', y') = (kx, ky)\): \[ A'(1 \times 2, 2 \times 2) = (2,4), \] \[ B'(4 \times 2, 2 \times 2) = (8,4), \] \[ C'(4 \times 2, 5 \times 2) = (8,10), \] \[ D'(1 \times 2, 5 \times 2) = (2,10). \] Thus, the enlarged rectangle has vertices **\(A'(2,4)\), \(B'(8,4)\), \(C'(8,10)\), and \(D'(2,10)\)**.

Example 4: Shearing a Parallelogram

A parallelogram has vertices \(A(1,1)\), \(B(4,1)\), \(C(5,4)\), and \(D(2,4)\). It is subjected to a horizontal shear transformation with shear factor \(k=2\) along the \(x\)-axis. Find the new coordinates.

Solution:

Using the shear transformation formula: \[ (x', y') = (x + ky, y). \] Applying the shear to each vertex: \[ A'(1 + 2(1), 1) = (3,1), \] \[ B'(4 + 2(1), 1) = (6,1), \] \[ C'(5 + 2(4), 4) = (13,4), \] \[ D'(2 + 2(4), 4) = (10,4). \] Thus, the sheared parallelogram has vertices **\(A'(3,1)\), \(B'(6,1)\), \(C'(13,4)\), and \(D'(10,4)\)**.