3.5 Mensuration

Mensuration involves calculating lengths, areas, surface areas, and volumes of various geometric shapes. It is divided into two categories: 2D shapes (plane figures) and 3D shapes (solids).

Key Concepts:

1. Areas and Perimeters of 2D Shapes:

• Triangle:

  \[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height}, \quad \text{Perimeter} = a + b + c, \] where \(a, b, c\) are the lengths of the sides.

• Square:

  \[ \text{Area} = \text{side}^2, \quad \text{Perimeter} = 4 \times \text{side}. \]

• Rectangle:

  \[ \text{Area} = \text{length} \times \text{breadth}, \quad \text{Perimeter} = 2 \times (\text{length} + \text{breadth}). \]

• Trapezium:

  \[ \text{Area} = \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}. \]

• Parallelogram:

  \[ \text{Area} = \text{base} \times \text{height}, \quad \text{Perimeter} = 2 \times (\text{length} + \text{breadth}). \]

• Circle:

  \[ \text{Area} = \pi r^2, \quad \text{Circumference} = 2\pi r, \] where \(r\) is the radius.

• Circular Segment:

  \[ \text{Area of Segment} = \frac{r^2}{2}(\theta - \sin\theta), \quad \text{Arc Length} = r\theta, \] where \(r\) is the radius and \(\theta\) is the angle in radians.

2. Surface Areas and Volumes of 3D Shapes:

• Cube:

  \[ \text{Surface Area} = 6a^2, \quad \text{Volume} = a^3, \] where \(a\) is the side length.

• Cuboid:

  \[ \text{Surface Area} = 2(lb + bh + hl), \quad \text{Volume} = l \times b \times h, \] where \(l, b, h\) are the length, breadth, and height.

• Cylinder:

  \[ \text{Curved Surface Area} = 2\pi rh, \quad \text{Total Surface Area} = 2\pi r(h + r), \quad \text{Volume} = \pi r^2h, \] where \(r\) is the radius and \(h\) is the height.

• Cone:

  \[ \text{Curved Surface Area} = \pi rl, \quad \text{Total Surface Area} = \pi r(l + r), \quad \text{Volume} = \frac{1}{3}\pi r^2h, \] where \(r\) is the radius, \(h\) is the height, and \(l\) is the slant height.

• Sphere:

  \[ \text{Surface Area} = 4\pi r^2, \quad \text{Volume} = \frac{4}{3}\pi r^3, \] where \(r\) is the radius.

Relation Between Mass, Density, and Volume:

The relationship is given by: \[ \text{Density} = \frac{\text{Mass}}{\text{Volume}}, \quad \text{Mass} = \text{Density} \times \text{Volume}. \]

Examples:

Example 1: Find the area and perimeter of a rectangle with length 8 cm and breadth 5 cm.

Solution:

Area: \[ \text{Area} = \text{length} \times \text{breadth} = 8 \times 5 = 40 \text{ cm}^2. \] Perimeter: \[ \text{Perimeter} = 2 \times (\text{length} + \text{breadth}) = 2 \times (8 + 5) = 26 \text{ cm}. \] Therefore, the area is \(40 \text{ cm}^2\) and the perimeter is \(26 \text{ cm}\).

Example 2: Calculate the volume and total surface area of a sphere with radius 7 cm.

Solution:

Volume: \[ \text{Volume} = \frac{4}{3}\pi r^3 = \frac{4}{3}\pi (7)^3 = \frac{4}{3} \times \pi \times 343 \approx 1436.76 \text{ cm}^3. \] Surface Area: \[ \text{Surface Area} = 4\pi r^2 = 4 \times \pi \times (7)^2 = 4 \times \pi \times 49 \approx 615.75 \text{ cm}^2. \] Therefore, the volume is approximately \(1436.76 \text{ cm}^3\) and the surface area is approximately \(615.75 \text{ cm}^2\).

Example 3: Find the mass of a cylindrical object with radius 3 cm, height 10 cm, and density \(8 \text{ g/cm}^3\).

Solution:

Volume: \[ \text{Volume} = \pi r^2 h = \pi (3)^2 (10) = 90\pi \approx 282.74 \text{ cm}^3. \] Mass: \[ \text{Mass} = \text{Density} \times \text{Volume} = 8 \times 282.74 = 2261.92 \text{ g}. \] Therefore, the mass is approximately \(2261.92 \text{ g}\).

Example 4: In the diagram below, the radius of the sector of circle center \(O\) is \(7 \, \text{cm}\) and \(\angle MON = 60^\circ\). Find, correct to one decimal place, the area of the shaded portion. (Take \(\pi = \frac{22}{7}\)).

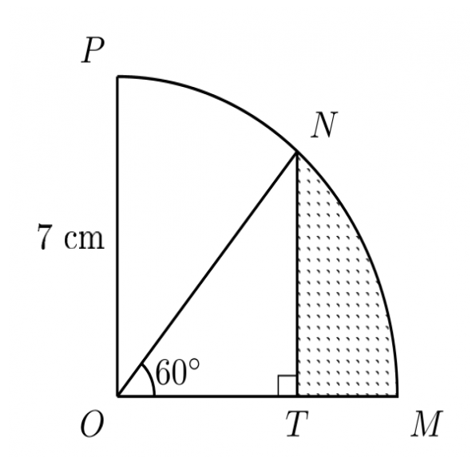
Solution:

Step 1: Calculate the area of the sector: \[ \text{Area of the sector} = \frac{\theta}{360^\circ} \times \pi r^2. \] Substitute \(\theta = 60^\circ\), \(r = 7\), and \(\pi = \frac{22}{7}\): \[ \text{Area of the sector} = \frac{60}{360} \times \frac{22}{7} \times 7^2. \] Simplify: \[ \text{Area of the sector} = \frac{1}{6} \times \frac{22}{7} \times 49 = \frac{22 \times 49}{42} = \frac{1078}{42} \approx 25.7 \, \text{cm}^2. \] Step 2: Calculate the area of \(\triangle OMT\): Since \(\triangle OMT\) is a right triangle: \[ \text{Area of } \triangle OMT = \frac{1}{2} \times \text{base} \times \text{height}. \] Here, \(\text{base} = 7 \, \text{cm}\) and \(\text{height} = 7 \, \text{cm}\): \[ \text{Area of } \triangle OMT = \frac{1}{2} \times 7 \times 7 = 24.5 \, \text{cm}^2. \] Step 3: Find the area of the shaded portion: \[ \text{Area of shaded portion} = \text{Area of sector} - \text{Area of } \triangle OMT. \] Substitute: \[ \text{Area of shaded portion} = 25.7 - 24.5 = 1.2 \, \text{cm}^2. \] Therefore, the area of the shaded portion is approximately \(1.2 \, \text{cm}^2\).