3.2 Circles

Circles are fundamental shapes in geometry and have unique properties and theorems associated with them. Below are key concepts and theorems related to circles.

Key Concepts:

• Radius and Diameter:

  The radius is the distance from the center of the circle to any point on its circumference. The diameter is twice the radius.

• Circumference:

  The perimeter of a circle is given by the formula: \[ C = 2\pi r, \] where \(r\) is the radius.

• Area:

  The area of a circle is given by: \[ A = \pi r^2. \]

• Tangent:

  A tangent to a circle is a line that touches the circle at exactly one point. The radius at the point of tangency is perpendicular to the tangent.

• Chord:

  A chord is a line segment with endpoints on the circle. The perpendicular from the center to a chord bisects the chord.

• Arc and Sector:

  An arc is a part of the circumference, and a sector is the region enclosed by two radii and an arc.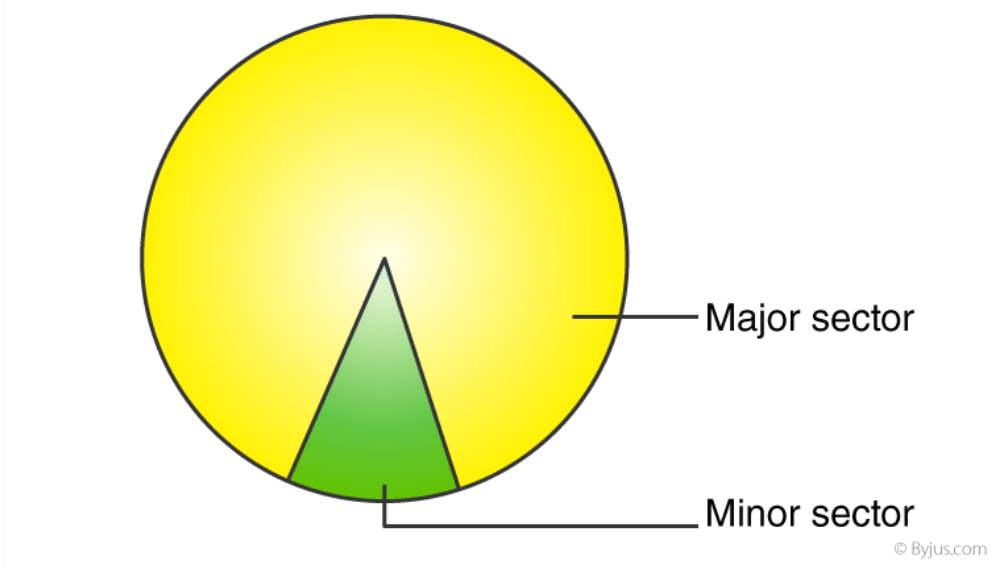
  
  

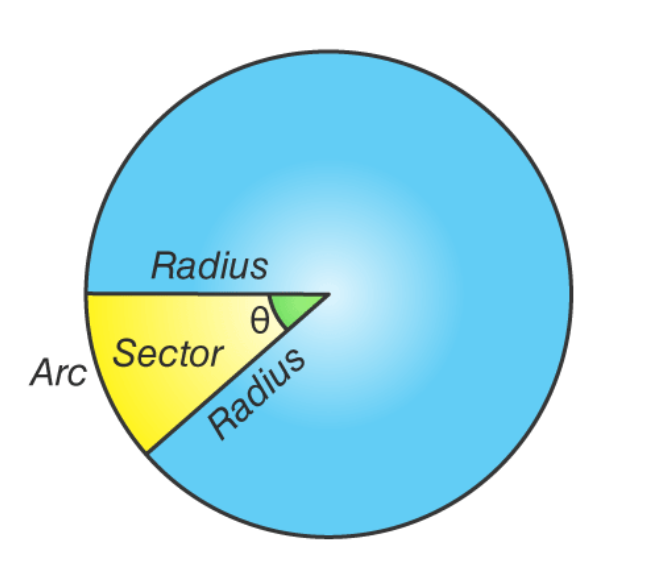
• Area of an sector and Arc length:

  \[ \text{Area of Sector} = \frac{\theta}{360^\circ} \times \pi r^2, \] \[ \text{Arc Length} = \frac{\theta}{360^\circ} \times 2\pi r, \] where \(\theta\) is the central angle in degrees and \(r\) is the radius of the circle.

Circle Theorems:

• Angle at the Center:

  The angle subtended by an arc at the center of a circle is twice the angle subtended at any point on the circumference.

• Angle in a Semicircle:

  The angle subtended by a diameter at the circumference is a right angle.

• Cyclic Quadrilateral:

  The opposite angles of a cyclic quadrilateral (a quadrilateral inscribed in a circle) are supplementary.

• Tangent-Secant Theorem:

  If a tangent and a secant are drawn from an external point, then the square of the length of the tangent is equal to the product of the secant's external and total lengths.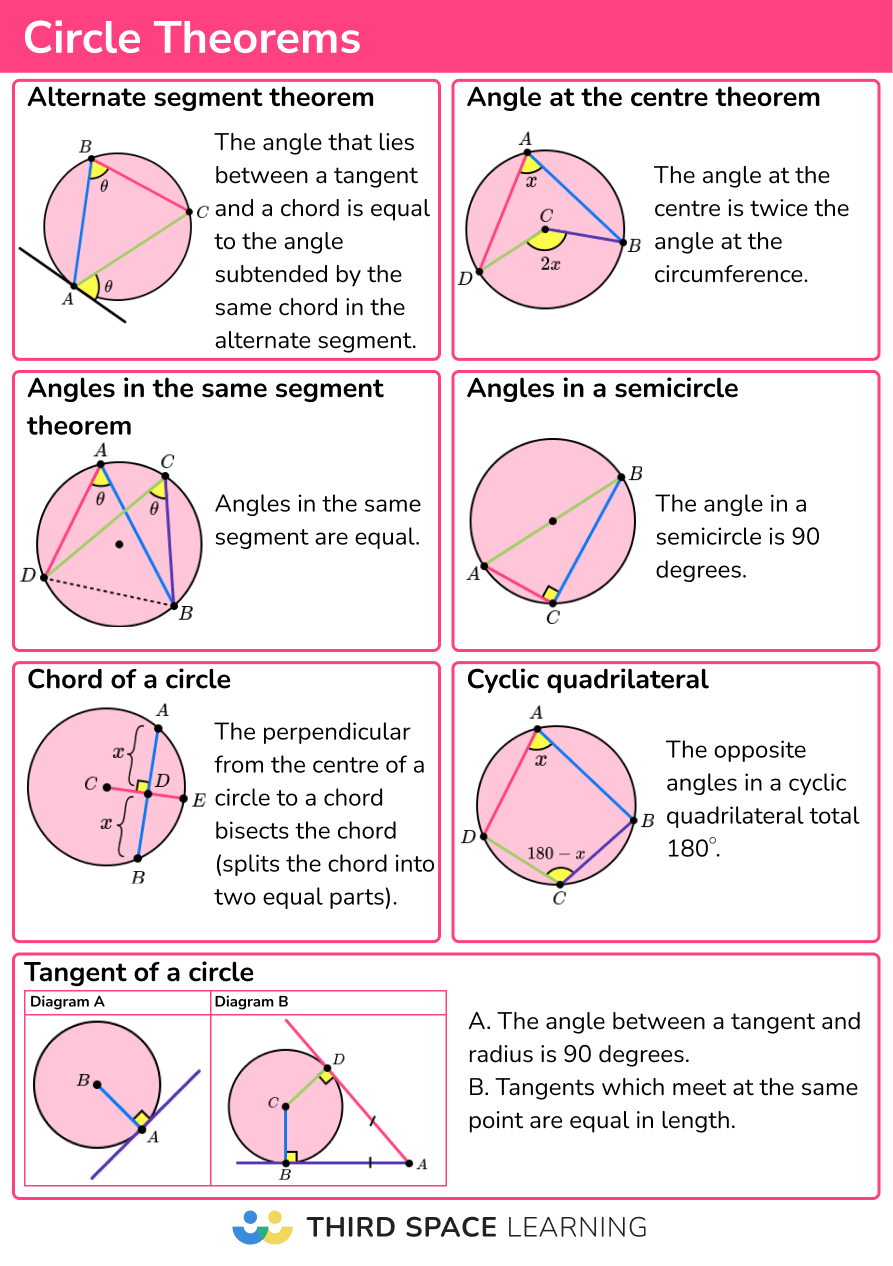
  

Examples:

Example 1: Find the circumference of a circle with radius 7 cm.

Solution:

Use the formula for circumference: \[ C = 2\pi r = 2 \times \pi \times 7 = 14\pi \approx 43.98 \text{ cm}. \] Therefore, the circumference is approximately \(43.98\) cm.

Example 2: A chord of a circle is 12 cm long, and its distance from the center is 5 cm. Find the radius of the circle.

Solution:

Let the radius be \(r\). Using the Pythagoras theorem in the triangle formed by the radius, half the chord, and the perpendicular distance: \[ r^2 = 6^2 + 5^2 = 36 + 25 = 61. \] \[ r = \sqrt{61} \approx 7.81 \text{ cm}. \] Therefore, the radius of the circle is approximately \(7.81\) cm.

Example 3: Prove that the angle subtended by a diameter at the circumference is a right angle.

Solution:

Let \(ABC\) be a triangle inscribed in a circle, where \(AB\) is the diameter. By the angle at the center theorem: \[ \text{Angle at the center } \angle AOB = 180^\circ. \] \[ \text{Angle at the circumference } \angle ACB = \frac{1}{2} \times 180^\circ = 90^\circ. \] Therefore, the angle subtended by a diameter is always a right angle.

Example 4: Find the area of a sector with radius 6 cm and central angle \(60^\circ\).

Solution:

Use the formula for the area of a sector: \[ A = \frac{\theta}{360^\circ} \times \pi r^2 = \frac{60^\circ}{360^\circ} \times \pi \times 6^2. \] Simplify: \[ A = \frac{1}{6} \times \pi \times 36 = 6\pi \approx 18.85 \text{ cm}^2. \] Therefore, the area of the sector is approximately \(18.85 \text{ cm}^2\).

Example 5: In the diagram below, \(O\) is the center of the circle \(QRS\) and \(\angle SQR = 28^\circ\). Find \(\angle ORS\).

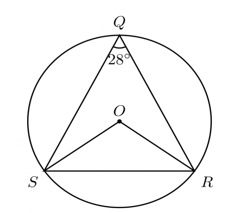
Solution:

Step 1: Recall the Circle Theorem for angles at the center and circumference: The angle subtended by an arc at the center of a circle is twice the angle subtended at the circumference by the same arc. Step 2: Identify the arc and the angles: - \(\angle SQR\) is the angle subtended at the circumference by the arc \(SR\). - \(\angle SOR\) is the angle subtended at the center by the same arc. Step 3: Use the Circle Theorem: \[ \angle SOR = 2 \times \angle SQR. \] Substitute \(\angle SQR = 28^\circ\): \[ \angle SOR = 2 \times 28^\circ = 56^\circ. \] Step 4: Find \(\angle ORS\): Since \(\triangle OSR\) is an isosceles triangle (radii \(OS\) and \(OR\) are equal), the base angles are equal: \[ \angle ORS = \angle OSR = \frac{180^\circ - \angle SOR}{2}. \] Substitute \(\angle SOR = 56^\circ\): \[ \angle ORS = \frac{180^\circ - 56^\circ}{2} = \frac{124^\circ}{2} = 62^\circ. \] Therefore, \(\angle ORS = 62^\circ\).