3.1 Plane Geometry
Plane geometry deals with shapes, lines, and angles in two-dimensional space. Understanding the properties of various geometric figures is fundamental to solving problems in geometry.Key Concepts:
Triangle and its Properties:
A triangle is a three-sided polygon with three angles. The sum of the interior angles of a triangle is always \(180^\circ\). Triangles can be classified based on their sides (scalene, isosceles, equilateral) or angles (acute, right, obtuse). The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Pythagoras Theorem:
In a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically: \[ c^2 = a^2 + b^2, \] where \(c\) is the hypotenuse, and \(a\) and \(b\) are the other two sides.Quadrilaterals and Their Properties:
A quadrilateral is a four-sided polygon with four angles. Common types include squares, rectangles, parallelograms, trapeziums, and rhombuses. The sum of the interior angles of a quadrilateral is \(360^\circ\). Specific properties include:- Opposite sides of a rectangle and parallelogram are equal.
- Diagonals of a square bisect each other at right angles.
- A trapezium has one pair of parallel sides.
Inscribed Triangles and Polygons:
An inscribed polygon is one whose vertices all lie on a single circle, called the circumcircle. The center of this circle is called the circumcenter, and the radius is the circumradius. For inscribed triangles, the angle subtended by a diameter at the circumference is always a right angle.Internal and External Angles of Triangles and Polygons:
The sum of the internal angles of a polygon with \(n\) sides is: \[ (n-2) \times 180^\circ. \] The sum of the external angles of any polygon is always \(360^\circ\), making each exterior angle equal to \[ \frac{360^\circ}{n}. \]Polygons and Their Properties:
Polygons are closed figures with three or more sides. Regular polygons have equal sides and angles. Examples include pentagons, hexagons, and octagons. The measure of each internal angle of a regular polygon with \(n\) sides is: \[ \frac{(n-2) \times 180^\circ}{n}. \]Examples:
Example 1: Calculate the hypotenuse of a right triangle with sides 3 cm and 4 cm.
Solution:
Use Pythagoras theorem: \[ c^2 = a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25. \] \[ c = \sqrt{25} = 5 \text{ cm}. \] Therefore, the hypotenuse is 5 cm.Example 2: Find the sum of the internal angles of a hexagon.
Solution:
For hexagon n=6.\\ Use the formula for the sum of internal angles of a polygon: \[ (n-2) \times 180^\circ = (6-2) \times 180^\circ = 4 \times 180^\circ = 720^\circ. \] Therefore, the sum of the internal angles of a hexagon is \(720^\circ\).Example 3: A square is inscribed in a circle. Find the radius of the circle if the side of the square is 8 cm.
Solution:
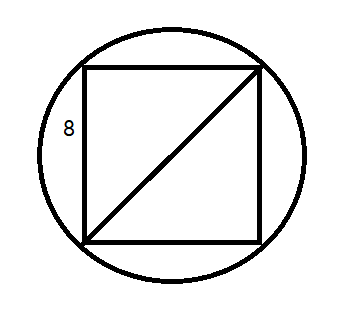
Example 4: Find each internal angle of a regular pentagon.
Solution:
Use the formula for each internal angle of a regular polygon with n=5: \[ \frac{(n-2) \times 180^\circ}{n} = \frac{(5-2) \times 180^\circ}{5} = \frac{3 \times 180^\circ}{5} = \frac{540^\circ}{5} = 108^\circ. \] Therefore, each internal angle of a regular pentagon is \(108^\circ\).