3.6 Loci

Loci are the set of points that satisfy a specific condition or rule. They are used to describe the path traced by moving points under given constraints in geometry.

Key Concepts:

• Definition of a Locus:

  A locus is the path traced by a point that moves according to a specific condition or rule.

• Some Standard Loci:

  • Locus of a Point at a Fixed Distance from Another Point:

    This is a circle with the fixed point as the center and the given distance as the radius.

  • Locus of Points Equidistant from Two Points:

    This is the perpendicular bisector of the line segment joining the two points. Perpendicular bisector to a line PQ is a line passing through midpoint of P and Q and perpendicular to PQ.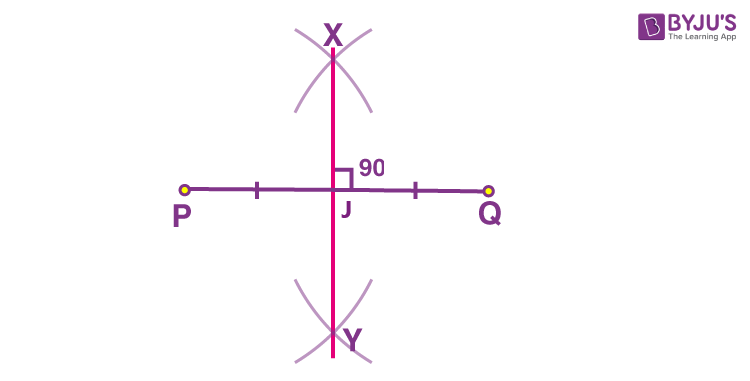
    

  • Locus of Points Equidistant from Two Intersecting Lines:

    This is the angle bisector of the angles formed by the intersecting lines.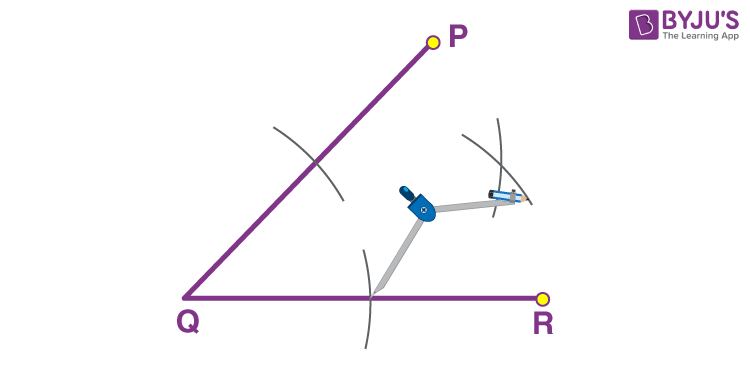
    

  • Locus of a Point at a Fixed Distance from a Line:

    This consists of two parallel lines at the given distance from the original line, one on either side.

• Real-Life Applications:

  Loci are applied in navigation, construction, and design to determine paths or boundaries.

Examples:

Example 1: Describe the locus of points equidistant from two fixed points \(A\) and \(B\).

Solution:

The locus of points equidistant from \(A\) and \(B\) is the perpendicular bisector of the line segment joining \(A\) and \(B\).

Example 2: Describe the locus of points equidistant from two intersecting lines.

Solution:

The locus of points equidistant from two intersecting lines is the pair of angle bisectors of the angles formed by the lines.

Example 3: A point \(P\) moves such that it is always \(5 \, \text{cm}\) away from a fixed point \(O\). Describe and sketch the locus of \(P\).

Solution:

The locus of \(P\) is a circle with center \(O\) and radius \(5 \, \text{cm}\).

Example 4: A point \(P\) moves such that it is always \(3 \, \text{cm}\) away from a straight line \(L\). Describe and sketch the locus of \(P\).

Solution:

The locus of \(P\) consists of two parallel lines, each \(3 \, \text{cm}\) away from \(L\), one on each side.

Example 5: A point \(P\) moves such that it is equidistant from two fixed points \(A\) and \(B\) and also equidistant from two intersecting lines \(L_1\) and \(L_2\). Describe the locus of \(P\).

Solution:

The locus of \(P\) is the intersection of the perpendicular bisector of the line segment \(AB\) and the angle bisectors of the angles formed by the intersecting lines \(L_1\) and \(L_2\).