3.3 Longitude and Latitude Problems, Bearings

Longitude and latitude are used to specify the position of points on the Earth's surface. Bearings and directions play a crucial role in navigation and solving geographical problems.

Key Concepts:

• Bearing of an Angle:

  Bearings are used to describe the direction of one point relative to another. Bearings are measured clockwise from the north direction and are usually expressed in three digits. For example, \(045^\circ\) represents a bearing of \(45^\circ\) from north.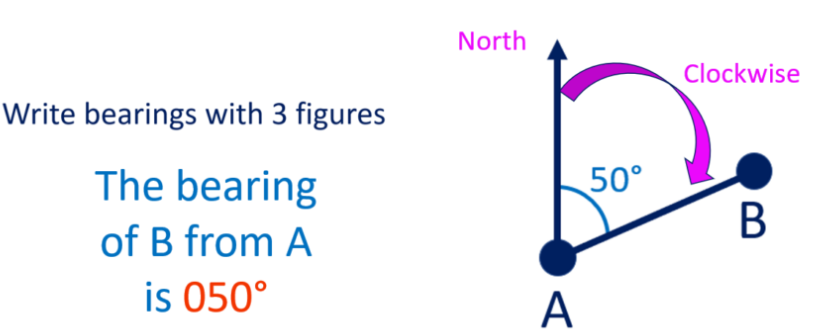
  

• Main Directions:

  The primary compass directions are:

  • North (N):

    \(0^\circ\) or \(360^\circ\)

  • East (E):

    \(90^\circ\)

  • South (S):

    \(180^\circ\)

  • West (W):

    \(270^\circ\)

Examples:

Example 1: A ship travels on a bearing of \(120^\circ\). What direction is the ship moving?

Solution:

A bearing of \(120^\circ\) is measured clockwise from north. This places the direction in the southeast quadrant. Therefore, the ship is moving southeast.

Example 2: Find the bearing from Point A to Point B if A is due west of B.

Solution:

If A is due west of B, the bearing from A to B is measured clockwise from north: \[ \text{Bearing} = 270^\circ. \] Therefore, the bearing is \(270^\circ\).

Example 3: John was facing \(S35^\circ E\). If he turned \(90^\circ\) in the anticlockwise direction, find his new direction.

Solution:

Step 1: Convert \(S35^\circ E\) to a bearing: \[ \text{Bearing} = 180^\circ - 35^\circ = 145^\circ. \] Step 2: Subtract \(90^\circ\) for the anticlockwise turn: \[ 145^\circ - 90^\circ = 55^\circ. \] Step 3: Convert the bearing back to a compass direction: \[ 55^\circ \text{ is measured as } N55^\circ E. \] Therefore, John's new direction is \(N55^\circ E\) (bearing of \(55^\circ\)).

Example 3:

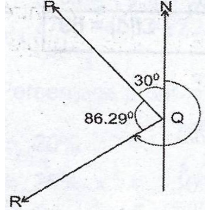
The bearing of \(Q\) from \(P\) is \(015^\circ\) and the bearing of \(P\) from \(R\) is \(015^\circ\). If \(Q\) and \(R\) are \(24\) km and \(32\) km respectively from \(P\): \begin{enumerate}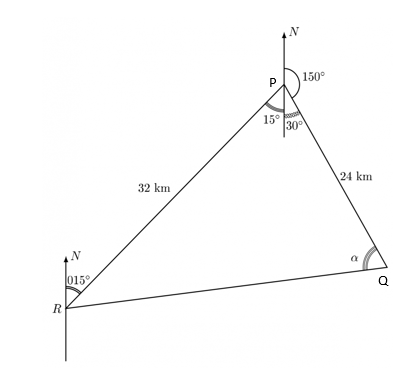

[(i)] Represent this information in a diagram.

[(ii)] Calculate the distance between \(Q\) and \(R\), correct to two decimal places.

[(iii)] Find the bearing of \(R\) from \(Q\), correct to the nearest degree. \end{enumerate}

Solution:

Step 1: Represent the given bearings in a diagram. Since both bearings are measured from the north, we construct a diagram accordingly. Step 2: Use the cosine rule to find the distance between \(Q\) and \(R\). The angle between \(PQ\) and \(PR\) is: \[ \theta = (15^\circ + 35^\circ) = 145^\circ. \] Using the cosine rule: \[ |QR|^2 = 32^2 + 24^2 - 2 \times 32 \times 24 \times \cos 45^\circ \] \[ |QR|^2 = 1024 + 576 - 1536 \cos 45^\circ \] \[ = 1600 - 1086.1056 \] \[ |QR|^2 = 513.8944 \] \[ |QR| = \sqrt{513.8944} = 22.669 \text{ km} \] \[ \approx 22.67 \text{ km to 2 dp} \] Step 3: Find the angle \(\angle\) PQR using the sine rule: \[ \frac{32}{\sin \angle PQR} = \frac{22.67}{\sin 45^\circ} \] \[ \sin \angle PQR = \frac{32 \times \sin 45^\circ}{22.67} \] \[ = 0.9981 \] \[ \angle PQR = \sin^{-1} (0.9981) = 86.4787^\circ \] Step 4: Calculate the bearing of \(R\) from \(Q\): \\

The bearing of R from Q is given by the reflex angle NQR. Thus, \[ \text{Reflex } \angle NQR = 360^\circ - (86.47^\circ + 30^\circ) \] \[ = 360^\circ - 116.47^\circ \] \[ = 243.53^\circ \] Hence, the bearing of R from Q: \[ \approx 244^\circ \quad (\text{to the nearest degree}) \]