4.3 Angles of Elevation and Depression, bearing
Angles of elevation and depression are used to describe the inclination or declination of a line of sight relative to the horizontal plane.Key Concepts:
-
Angle of Elevation:
The angle between the horizontal line and the line of sight when an observer looks up at an object. -
Angle of Depression:
The angle between the horizontal line and the line of sight when an observer looks down at an object.
Examples:
Example 1: A person standing 50 m away from a tower observes the top of the tower at an angle of elevation of \(35^\circ\). Find the height of the tower.
Solution:
Step 1: Identify the known values: - The horizontal distance to the tower is 50 m. - The angle of elevation is \(35^\circ\). - The height of the tower is the opposite side. Step 2: Use the tangent function: \[ \tan 35^\circ = \frac{\text{height}}{\text{distance}}. \] \[ \tan 35^\circ = \frac{h}{50}. \] Step 3: Solve for \(h\): \[ h = 50 \times \tan 35^\circ. \] Using \(\tan 35^\circ \approx 0.7002\): \[ h = 50 \times 0.7002 = 35.01 \text{ m}. \] Thus, the height of the tower is approximately \(35.0\) m.Example 2: A pilot at an altitude of 2 km observes an airport at an angle of depression of \(20^\circ\). Find the horizontal distance from the airplane to the airport.
Solution:
Step 1: Identify the known values: - The altitude (vertical height) is 2 km. - The angle of depression is \(20^\circ\). - The horizontal distance is the adjacent side. Step 2: Use the tangent function: \[ \tan 20^\circ = \frac{\text{altitude}}{\text{horizontal distance}}. \] \[ \tan 20^\circ = \frac{2}{d}. \] Step 3: Solve for \(d\): \[ d = \frac{2}{\tan 20^\circ}. \] Using \(\tan 20^\circ \approx 0.3640\): \[ d = \frac{2}{0.3640} \approx 5.49 \text{ km}. \] Thus, the horizontal distance is approximately \(5.49\) km.Example 3: A boat is sailing towards a lighthouse. When the boat is 300 m from the lighthouse, the angle of elevation to the top of the lighthouse is \(25^\circ\). If the height of the lighthouse is 60 m, find the distance from the top of the lighthouse to the boat.
Solution:
Step 1: Identify the known values: - The horizontal distance is 300 m. - The height of the lighthouse is 60 m. - The required distance is the hypotenuse. Step 2: Use the sine function: \[ \sin 25^\circ = \frac{60}{d}. \] Step 3: Solve for \(d\): \[ d = \frac{60}{\sin 25^\circ}. \] Using \(\sin 25^\circ \approx 0.4226\): \[ d = \frac{60}{0.4226} \approx 142.02 \text{ m}. \] Thus, the distance from the top of the lighthouse to the boat is approximately \(142.0\) m.Example 3:
The bearing of \(Q\) from \(P\) is \(015^\circ\) and the bearing of \(P\) from \(R\) is \(015^\circ\). If \(Q\) and \(R\) are \(24\) km and \(32\) km respectively from \(P\): \begin{enumerate}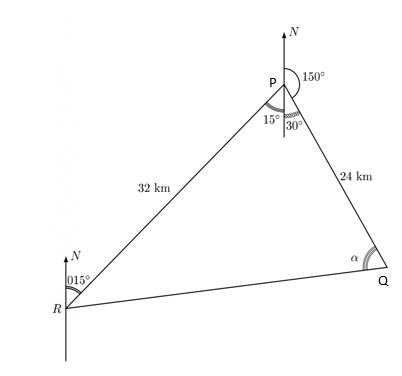
Solution:
Step 1: Represent the given bearings in a diagram. Since both bearings are measured from the north, we construct a diagram accordingly. Step 2: Use the cosine rule to find the distance between \(Q\) and \(R\). The angle between \(PQ\) and \(PR\) is: \[ \theta = (15^\circ + 35^\circ) = 145^\circ. \] Using the cosine rule: \[ |QR|^2 = 32^2 + 24^2 - 2 \times 32 \times 24 \times \cos 45^\circ \] \[ |QR|^2 = 1024 + 576 - 1536 \cos 45^\circ \] \[ = 1600 - 1086.1056 \] \[ |QR|^2 = 513.8944 \] \[ |QR| = \sqrt{513.8944} = 22.669 \text{ km} \] \[ \approx 22.67 \text{ km to 2 dp} \] Step 3: Find the angle \angle PQR using the sine rule: \[ \frac{32}{\sin \angle PQR} = \frac{22.67}{\sin 45^\circ} \] \[ \sin \angle PQR = \frac{32 \times \sin 45^\circ}{22.67} \] \[ = 0.9981 \] \[ \angle PQR = \sin^{-1} (0.9981) = 86.4787^\circ \] Step 4: Calculate the bearing of \(R\) from \(Q\): \\