4.1 Trigonometric Ratios and identities

Trigonometric ratios relate the angles and sides of right-angled triangles. The three primary trigonometric functions are sine, cosine, and tangent.

Key Concepts:

• Right-Angled Triangle Definition:

  In a right-angled triangle, the three sides are:
  • Hypotenuse: The longest side, opposite the right angle.
  • Opposite Side: The side opposite to the given angle.
  • Adjacent Side: The side next to the given angle (excluding the hypotenuse).

• Trigonometric Ratios:

  The three basic trigonometric ratios for an angle \(\theta\) in a right-angled triangle are: \[ \sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} \] \[ \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} \] \[ \tan \theta = \frac{\text{opposite}}{\text{adjacent}} \]
  
  \newpage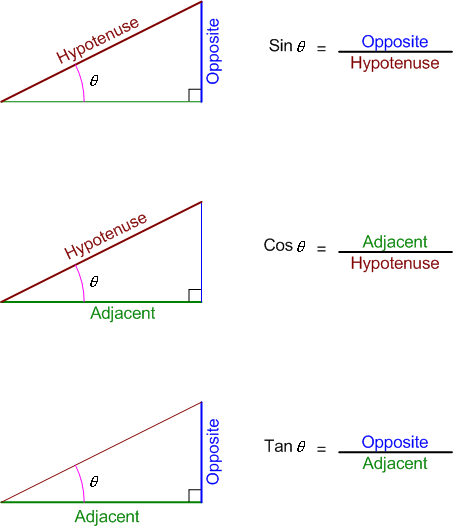

• Common Trigonometric Values:

  \[ \begin{array}{c|c|c|c} \theta & \sin \theta & \cos \theta & \tan \theta \\ \hline 0^\circ & 0 & 1 & 0 \\ 30^\circ & \frac{1}{2} & \frac{\sqrt{3}}{2} & \frac{1}{\sqrt{3}} \\ 45^\circ & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 1 \\ 60^\circ & \frac{\sqrt{3}}{2} & \frac{1}{2} & \sqrt{3} \\ 90^\circ & 1 & 0 & \text{undefined} \\ \end{array} \]

• Reciprocal Trigonometric Functions:

  • Cosecant: \(\csc \theta = \frac{1}{\sin \theta}\)
  • Secant: \(\sec \theta = \frac{1}{\cos \theta}\)
  • Cotangent: \(\cot \theta = \frac{1}{\tan \theta}\)

• Pythagorean Identity:

  \[ \sin^2 \theta + \cos^2 \theta = 1. \]

Examples:

Example 1: Given a right-angled triangle where \(\theta = 30^\circ\) and the hypotenuse is \(10\) cm, find the opposite and adjacent sides.

Solution:

Step 1: Use trigonometric ratios: \[ \sin 30^\circ = \frac{\text{opposite}}{\text{hypotenuse}}. \] Substituting values: \[ \frac{x}{10} = \frac{1}{2}. \] Solving for \(x\): \[ x = 10 \times \frac{1}{2} = 5 \text{ cm}. \] Step 2: Use the cosine function for the adjacent side: \[ \cos 30^\circ = \frac{\text{adjacent}}{\text{hypotenuse}}. \] \[ \frac{y}{10} = \frac{\sqrt{3}}{2}. \] Solving for \(y\): \[ y = 10 \times \frac{\sqrt{3}}{2} = 5\sqrt{3} \text{ cm}. \] Thus, the opposite side is \(5\) cm, and the adjacent side is \(5\sqrt{3}\) cm.

Example 2: A ladder is leaning against a vertical wall. The foot of the ladder is \(4\) m from the base of the wall, and the ladder makes an angle of \(60^\circ\) with the ground. Find the length of the ladder.

Solution:

Step 1: Identify the known values: - The adjacent side (distance from the wall) is \(4\) m. - The hypotenuse is the length of the ladder. - The angle given is \(60^\circ\). Step 2: Use the cosine function: \[ \cos 60^\circ = \frac{\text{adjacent}}{\text{hypotenuse}}. \] \[ \frac{4}{h} = \frac{1}{2}. \] Step 3: Solve for \(h\): \[ h = \frac{4}{\frac{1}{2}} = 8 \text{ m}. \] Thus, the ladder is \(8\) m long.

Example 3: Find \(\tan \theta\) if \(\sin \theta = 0.6\).

Solution:

Step 1: Use the Pythagorean identity: \[ \sin^2 \theta + \cos^2 \theta = 1. \] Substituting \(\sin \theta = 0.6\): \[ (0.6)^2 + \cos^2 \theta = 1. \] \[ 0.36 + \cos^2 \theta = 1. \] \[ \cos^2 \theta = 0.64. \] \[ \cos \theta = 0.8. \] Step 2: Use the tangent formula: \[ \tan \theta = \frac{\sin \theta}{\cos \theta}. \] \[ \tan \theta = \frac{0.6}{0.8} = 0.75. \] Thus, \(\tan \theta = 0.75\).

Example 4: Given that \(\cos x = \frac{12}{13}\), evaluate \(\frac{1 - \tan x}{\tan x}\).

Solution:

Step 1: Use the Pythagorean identity to find \(\sin x\): \[ \sin^2 x + \cos^2 x = 1. \] Substituting \(\cos x = \frac{12}{13}\): \[ \sin^2 x + \left(\frac{12}{13}\right)^2 = 1. \] \[ \sin^2 x + \frac{144}{169} = 1. \] \[ \sin^2 x = 1 - \frac{144}{169} = \frac{169}{169} - \frac{144}{169} = \frac{25}{169}. \] \[ \sin x = \frac{5}{13}. \] Step 2: Calculate \(\tan x\): \[ \tan x = \frac{\sin x}{\cos x} = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12}. \] Step 3: Evaluate \(\frac{1 - \tan x}{\tan x}\): \[ \frac{1 - \frac{5}{12}}{\frac{5}{12}}. \] Simplify the numerator: \[ 1 - \frac{5}{12} = \frac{12}{12} - \frac{5}{12} = \frac{7}{12}. \] Now, divide: \[ \frac{\frac{7}{12}}{\frac{5}{12}} = \frac{7}{12} \times \frac{12}{5} = \frac{7}{5}. \] Thus, the final answer is: \[ \frac{7}{5} \]