5.2 Measures of Central Tendency

Measures of central tendency describe the center of a data set using three main statistics: mean, median, and mode.

Key Concepts:

• Mean:

  The arithmetic average of a data set, calculated as: \[ \text{Mean} = \frac{\sum x f}{\sum f}, \] where \(x\) represents the class midpoint, and \(f\) is the frequency.\\ In case of grouped data use midpoints of each group to estimate the mean (see Example 2.)

• Median:

  The middle value in an ordered data set. Note that the data must be ordered first. \\
  • For an odd number of values: The median is the middle number. \\ Example: Data = \(1,2,3,4,5\) \\ Median = \(3\).
  • For an even number of values: The median is the average of the two middle numbers. \\ Example: Data = \(1,2,3,4,5,6\) \\ Median = \(\frac{3+4}{2} = 3.5\).

• Mode:

  The most frequently occurring value in a dataset. For grouped data, the modal class is the class with the highest frequency.
  • If a number appears most frequently, it is the mode. \\ Example: Data = \(1,2,2,3,2,4,5,6,4,3,2,3,4,2,3,2,6,5\) \\ Frequency:
    • \(1\) appears once.
    • \(2\) appears

      6

      times.
    • \(3\) appears 5 times.
    • \(4\) appears 3 times.
    • \(5\) appears 2 times.
    • \(6\) appears 2 times.
    Mode =

    2

    (most frequent value).

• Graph work:

  You can find certain measures of central tendency from cumulative frequency graph or histograms. See examples 3 and 4 for details.

Examples:

Example 1: Find the Mean, Median, and Mode of the Given Data Set.

Given Data:

\\ \(12, 7, 10, 15, 10, 18, 12, 10, 14, 7, 16, 12, 10, 9, 10\)

Solution:

Step 1: Find the Mode

• Count the frequency of each number:
  • \(7\) appears twice.
  • \(9\) appears once.
  • \(10\) appears

    5

    times.
  • \(12\) appears 3 times.
  • \(14\) appears once.
  • \(15\) appears once.
  • \(16\) appears once.
  • \(18\) appears once.
• The mode is the number that appears most frequently. \[ \text{Mode} = 10 \]

Step 2: Find the Median

• Arrange the data in ascending order: \[ 7, 7, 9, 10, 10, 10, 10, 10, 12, 12, 12, 14, 15, 16, 18 \]
• Find the middle value. Since there are 15 numbers (odd count), the median is the 8th value. \[ \text{Median} = 10 \]

Step 3: Find the Mean

• Use the mean formula: \[ \text{Mean} = \frac{\sum x}{n} \]
• Calculate the sum of all numbers: \[ 7 + 7 + 9 + 10 + 10 + 10 + 10 + 10 + 12 + 12 + 12 + 14 + 15 + 16 + 18 = 162 \]
• Divide by the total number of values (\(n=15\)):

Example 2: Find the mean from the following frequency distribution.

\begin{tabular}{c|c|c}

Class Interval

&

Frequency (f)

&

Midpoint (x)

\\ \hline 0 - 10 & 4 & 5 \\ 10 - 20 & 6 & 15 \\ 20 - 30 & 8 & 25 \\ 30 - 40 & 10 & 35 \\ 40 - 50 & 7 & 45 \\ \end{tabular}

Solution:

Using the formula: \[ \text{Mean} = \frac{\sum x f}{\sum f}. \] \[ \text{Mean} = \frac{(5 \times 4) + (15 \times 6) + (25 \times 8) + (35 \times 10) + (45 \times 7)}{4 + 6 + 8 + 10 + 7}. \] \[ = \frac{20 + 90 + 200 + 350 + 315}{35}. \] \[ = \frac{975}{35} = 27.86. \] Thus, the mean is approximately \(27.86\).

Example 3: Determine the median from the cumulative frequency curve (ogive) below.

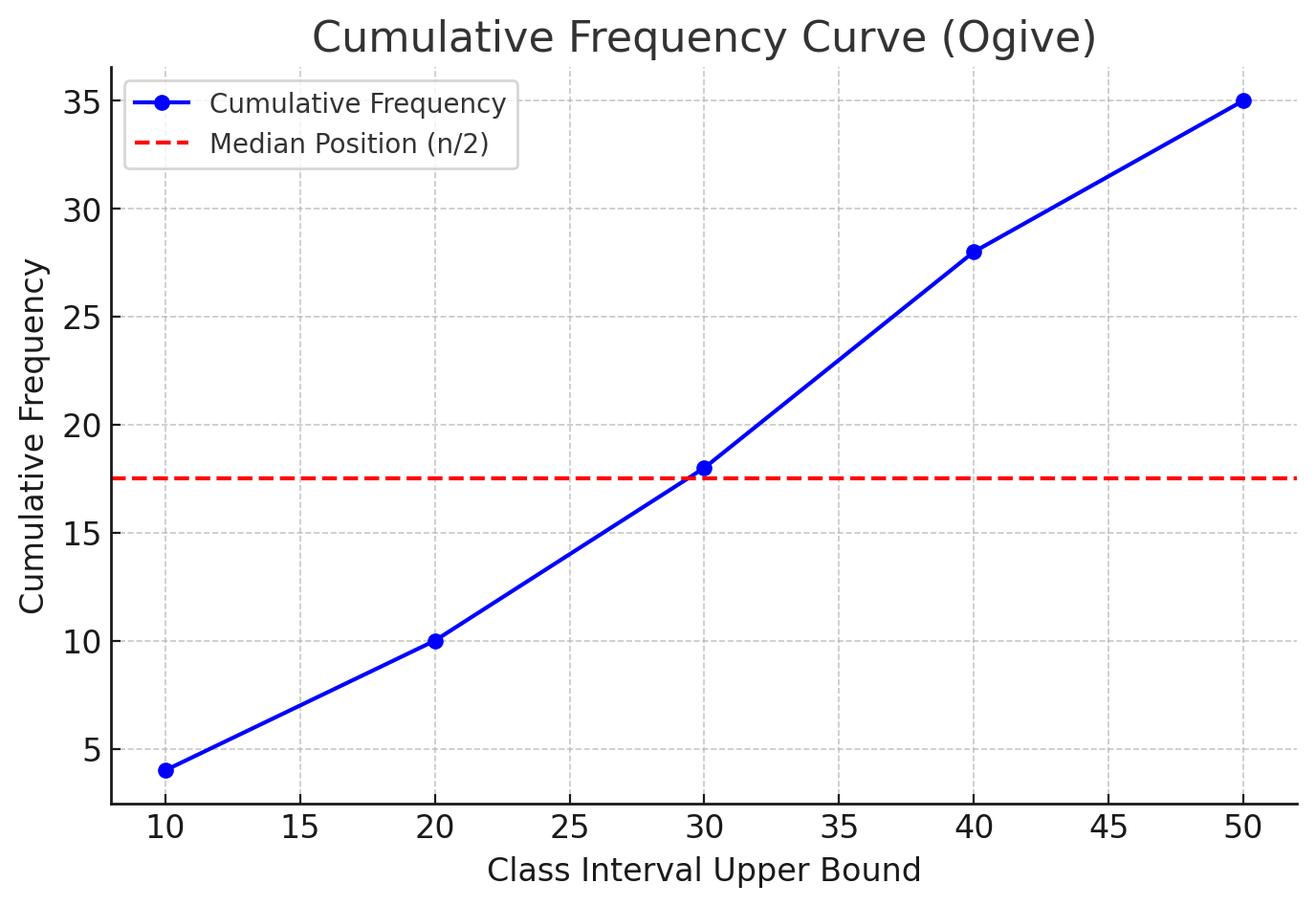
Solution:

Step 1: Identify the total number of observations \(n\). Step 2: Find the median position: \(\frac{n}{2} = \frac{35}{2}=17.5\). Step 3: Locate the corresponding value on the cumulative frequency curve: dashed red line on the graph. Step 4: Use interpolation if necessary to estimate the median value. Solution is the intersection of cummulative frequency curve and dashed line. From the graph, the estimated median is around \(28\).

Example 4: Determine the Mode from the Given Histogram.

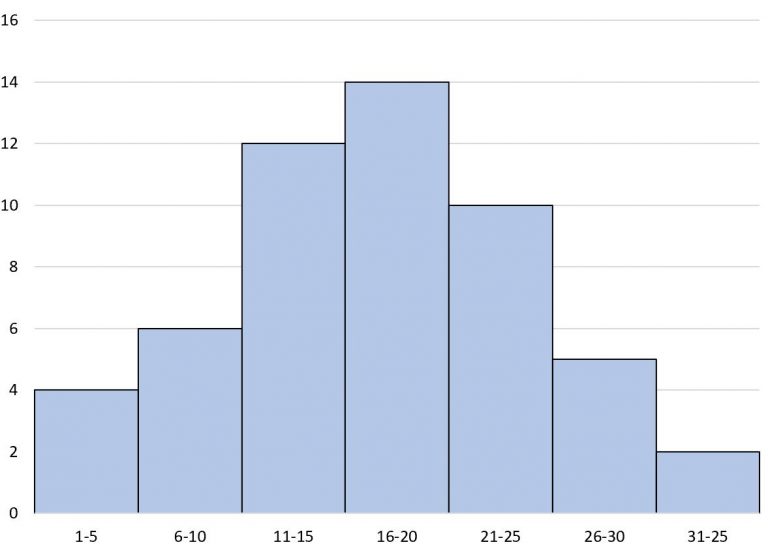
Solution:

Step 1: Identify the modal class.

• The modal class is the class interval with the highest frequency, which is \(16-20\).

Step 2: Use the histogram and the line intersection method.

• Draw two diagonal lines from the tops of the bars adjacent to the modal class, forming an "X" shape.
  
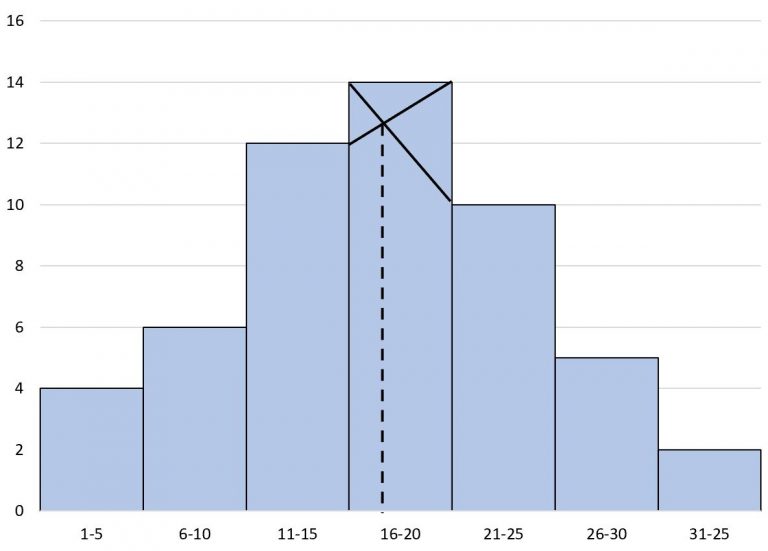
• The intersection of these lines falls near \(x \approx 17\), which represents the estimated mode.

Step 3: Conclusion.

• From the visual estimation, the mode is approximately: \[ \textbf{Mode} \approx 17. \]

Thus, the mode is visually estimated to be around 17.