6.3 Probability Calculations from Various Graphs

Probability can be estimated from different types of graphical representations, including pie charts, histograms, cumulative frequency graphs, and Venn diagrams.

Examples:

Example 1: Probability from a Pie Chart

A pie chart represents the distribution of students in a school by their favorite subjects: Mathematics (90°), Science (120°), English (60°), and Arts (90°). What is the probability that a randomly chosen student prefers Science?

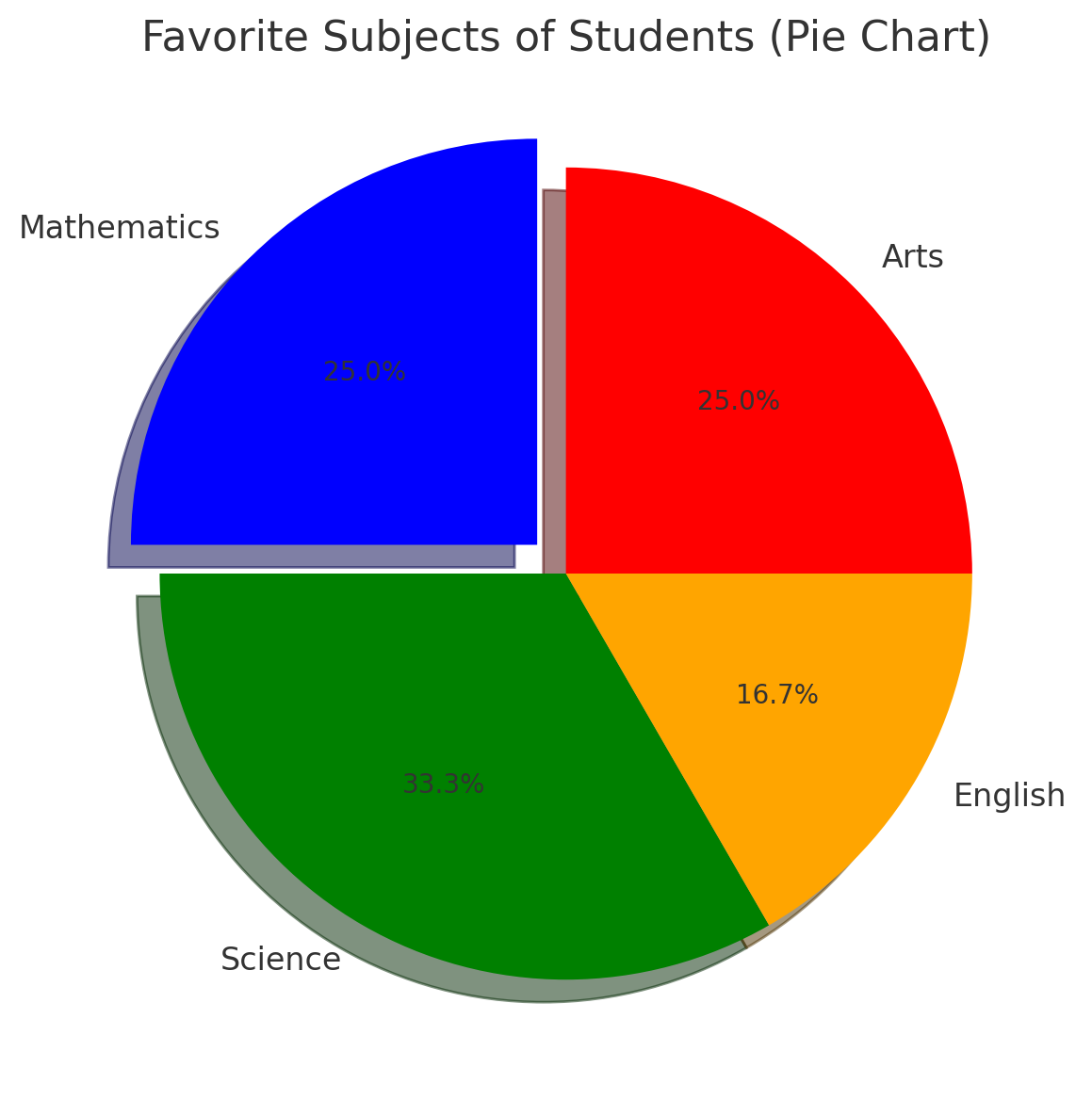
Solution:

Step 1: Compute the proportion of students who prefer Science. \[ \text{Fraction of Science} = \frac{120^\circ}{360^\circ} = \frac{1}{3}. \] Step 2: Compute probability. \[ P(\text{Science}) = \frac{1}{3} = 0.333. \] Thus, the probability that a randomly chosen student prefers Science is **\(0.333\) or \(33.3\%\)**.

Example 2: Probability from a Histogram

A histogram represents the number of students who scored different marks in a test. The total number of students is 100. Find the probability that a randomly chosen student scored between 70 and 80.

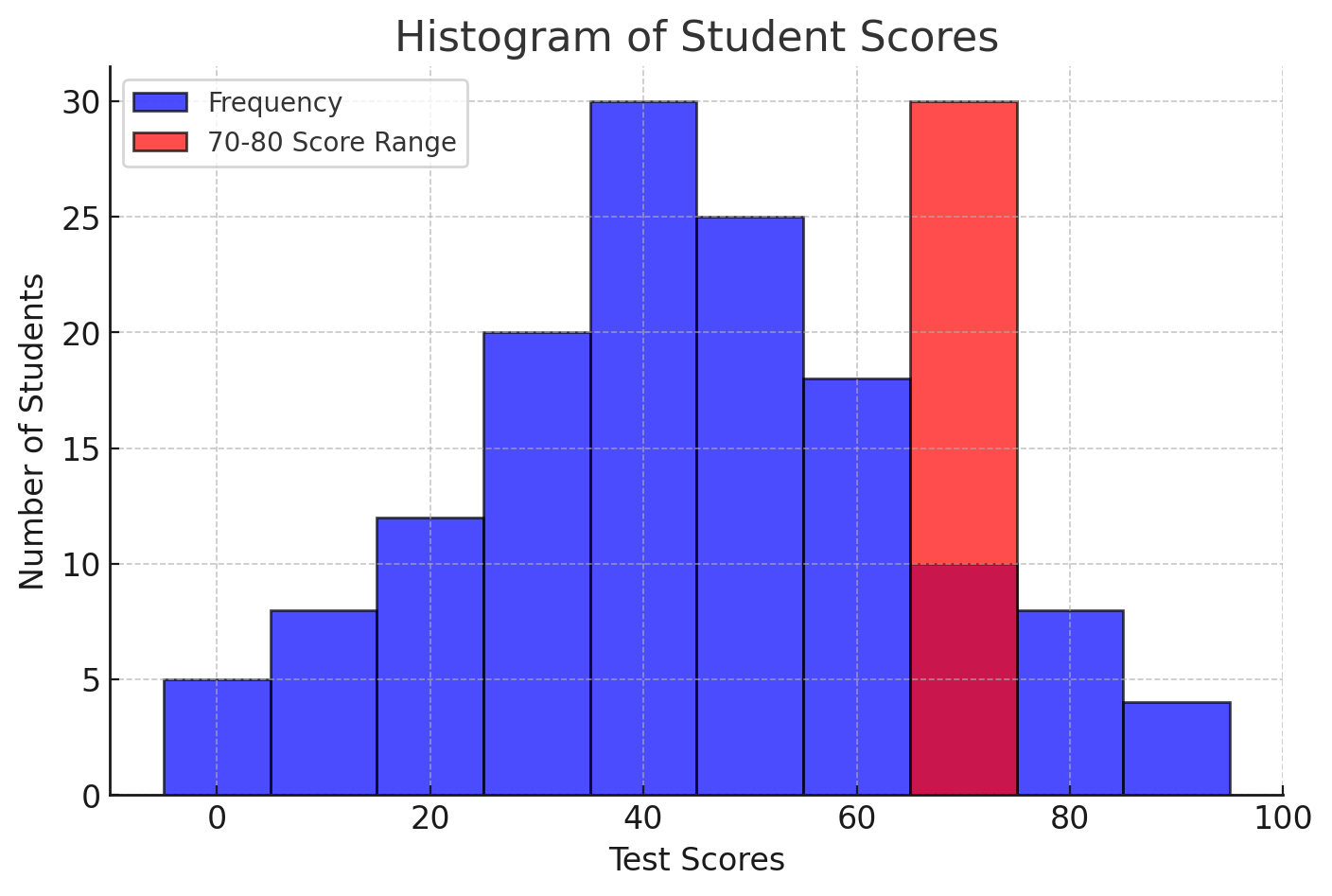
Solution:

Step 1: Use the probability formula. \[ P(70 \leq \text{Score} \leq 80) = \frac{\text{Number of students in range}}{\text{Total students}}. \] \[ = \frac{30}{100} = 0.30. \] Thus, the probability is **\(0.30\) or \(30\%\)**.

Example 3: Probability from a Cumulative Frequency Curve

A cumulative frequency graph shows the number of students scoring below certain marks in a test. Find the probability for the student to get distinction for the test if distinction score is 90.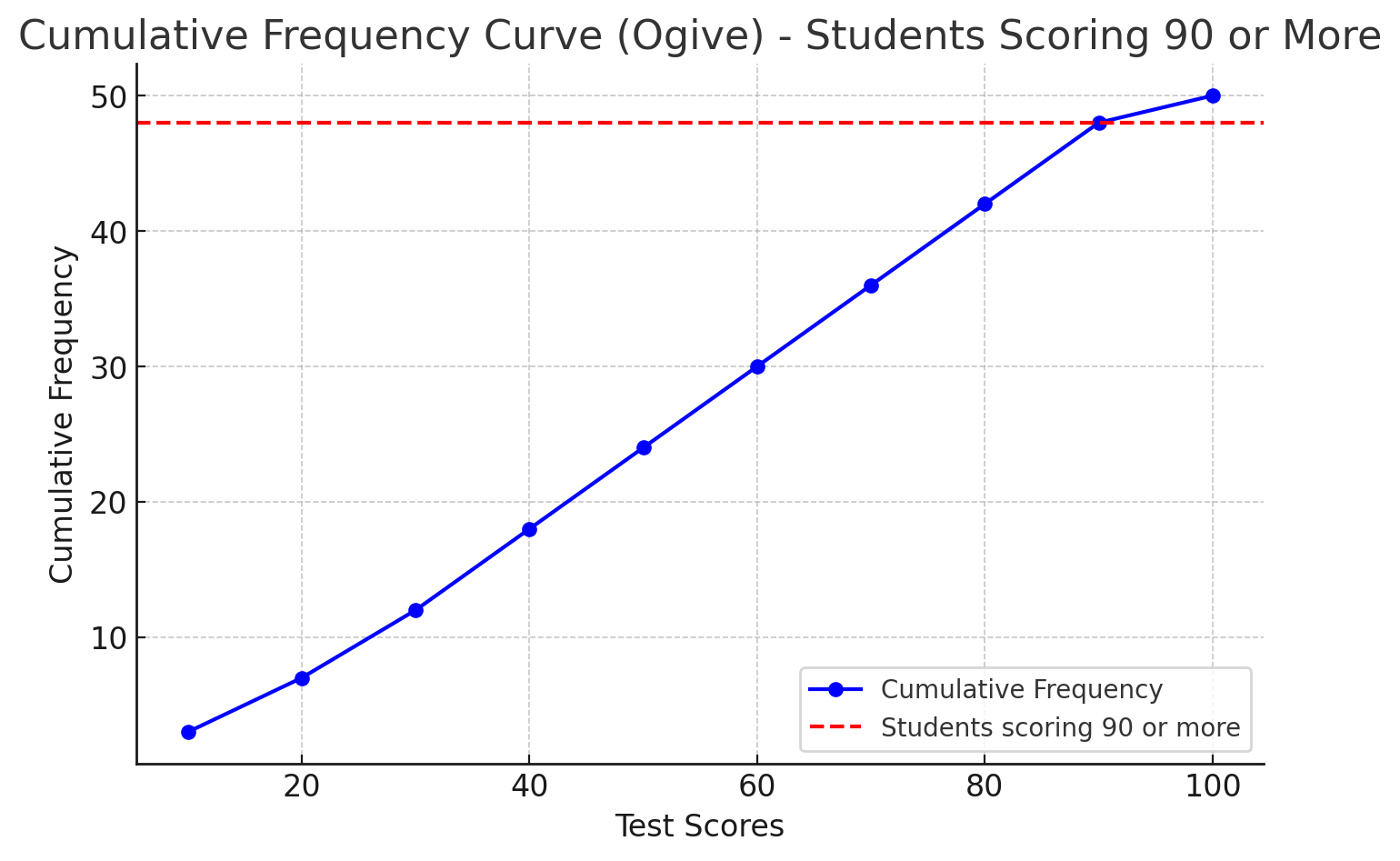

Solution:

Step 1: Compute probability. \[ P(distinction)=P(\text{Score} >90) = \frac{2}{50} = 0.04. \] Thus, the probability is **\(0.04\) or \(4\%\)**.

Example 4: Probability from a Venn Diagram

A Venn diagram shows the distribution of students who study Mathematics (40 students) and Science (50 students), with 20 students studying both subjects. Total number of studnets is 200. If a student is randomly selected, find \\ a)the probability that the student studies either Mathematics or Science.\\ b)the probability the study math only

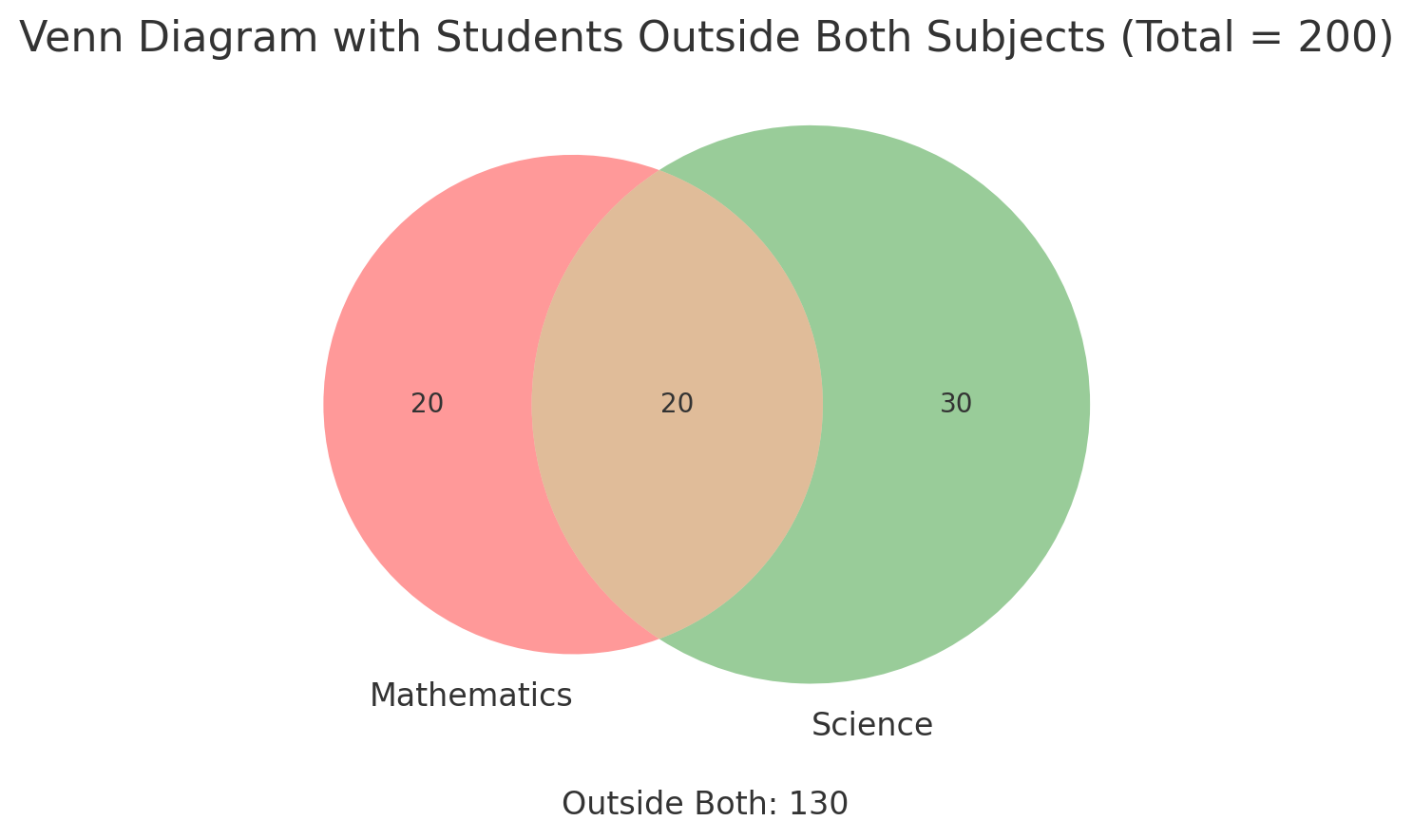
Part A Solution:

Step 1: Use the addition rule. \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \] \[ P(\text{Math or Science}) = \frac{40}{200} + \frac{50}{200} - \frac{20}{100}. \] \[ = \frac{70}{200} = 0.35. \] Thus, the probability is **\(0.35\) or \(35\%\)**.\\ \vspace{10pt}

Part B Solution:

\[ P(\text{Math Only}) = \frac{20}{200}=0.1. \] Thus, the probability is **\(0.10\) or \(10\%\)**.