6.2 Combination of Events
In probability, events can be combined using the **addition law** (for "or" situations) and the **multiplication law** (for "and" situations). Events can also be classified as **mutually exclusive** or **independent**.Key Concepts:
-
Addition Law of Probability:
Used for the probability of either event A or event B occurring. \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \]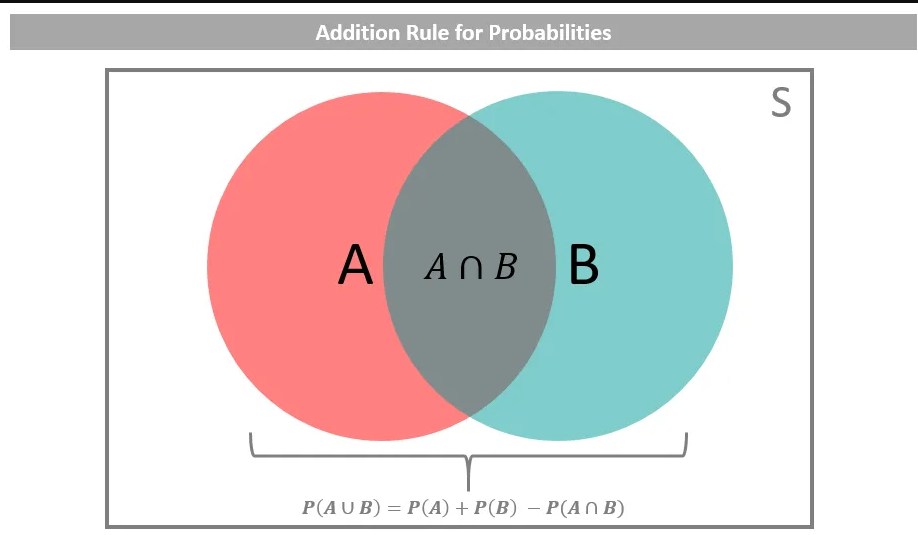
-
Mutually Exclusive Events:
Two events that cannot happen at the same time. \[ P(A \cap B) = 0. \] If A and B are mutually exclusive, then: \[ P(A \cup B) = P(A) + P(B). \] -
Independent Events:
The occurrence of one event does not affect the probability of the other. \[ P(A \cap B) = P(A) \times P(B). \]
Examples:
Example 1: Addition Rule with Overlapping Events
A deck of 52 cards contains 13 hearts and 13 face cards. If a card is drawn at random, what is the probability that it is a heart or a face card?Solution:
Step 1: Use the addition formula: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \] Step 2: Find the probabilities: \[ P(\text{Heart}) = \frac{13}{52}, \quad P(\text{Face Card}) = \frac{12}{52}. \] Since there are 3 face cards in hearts, \[ P(\text{Heart} \cap \text{Face Card}) = \frac{3}{52}. \] Step 3: Compute: \[ P(\text{Heart or Face Card}) = \frac{13}{52} + \frac{12}{52} - \frac{3}{52} = \frac{22}{52} = \frac{11}{26}. \]Example 2: Probability of Independent Events
A fair die is rolled, and a coin is flipped. What is the probability of getting a 4 on the die and heads on the coin?Solution:
Step 1: Identify the probabilities: \[ P(\text{Rolling a 4}) = \frac{1}{6}, \quad P(\text{Flipping Heads}) = \frac{1}{2}. \] Step 2: Since these are independent events, use the multiplication rule: \[ P(4 \cap H) = P(4) \times P(H) = \frac{1}{6} \times \frac{1}{2} = \frac{1}{12}. \]Example 3: Mutually Exclusive Events
A bag contains 5 red marbles and 7 blue marbles. If one marble is drawn at random, what is the probability that it is either red or blue?Solution:
Since drawing a red marble and drawing a blue marble are mutually exclusive events, we use: \[ P(A \cup B) = P(A) + P(B). \] \[ P(\text{Red}) = \frac{5}{12}, \quad P(\text{Blue}) = \frac{7}{12}. \] \[ P(\text{Red or Blue}) = \frac{5}{12} + \frac{7}{12} = 1. \] Since one of these must occur, the probability is 1.Example 4: Probability of Winning Independent Contracts
A building contractor tendered for two independent contracts, \(X\) and \(Y\). The probabilities that he will win contract \(X\) is 0.5 and not win contract \(Y\) is 0.3. What is the probability that he will: \begin{enumerate}Solution:
Let: \[ P(X) = 0.5, \quad P(\text{Not } Y) = 0.3. \] Since \(P(\text{Not } Y) = 0.3\), then: \[ P(Y) = 1 - 0.3 = 0.7. \](i) Probability of Winning Both Contracts:
Since the events are independent: \[ P(X \cap Y) = P(X) \times P(Y) = 0.5 \times 0.7 = 0.35. \](ii) Probability of Winning Exactly One Contract:
This occurs in two ways: - Wins \(X\) and loses \(Y\): \(P(X \cap \text{Not } Y) = P(X) \times P(\text{Not } Y)\). - Loses \(X\) and wins \(Y\): \(P(\text{Not } X \cap Y) = P(\text{Not } X) \times P(Y)\). Since \(P(\text{Not } X) = 1 - 0.5 = 0.5\), we compute: \[ P(X \cap \text{Not } Y) = 0.5 \times 0.3 = 0.15. \] \[ P(\text{Not } X \cap Y) = 0.5 \times 0.7 = 0.35. \] Adding both cases: \[ P(\text{Exactly one contract}) = 0.15 + 0.35 = 0.50. \](iii) Probability of Winning Neither Contract:
\[ P(\text{Not } X \cap \text{Not } Y) = P(\text{Not } X) \times P(\text{Not } Y). \] \[ = 0.5 \times 0.3 = 0.15. \]Final Answers:
- Probability of winning both contracts: \(0.35\).
- Probability of winning exactly one contract: \(0.50\).
- Probability of winning neither contract: \(0.15\).