1.10 Sets

Set theory is a fundamental branch of mathematics that deals with collections of objects, called sets. These objects are called elements or members of the set.

Key Concepts:

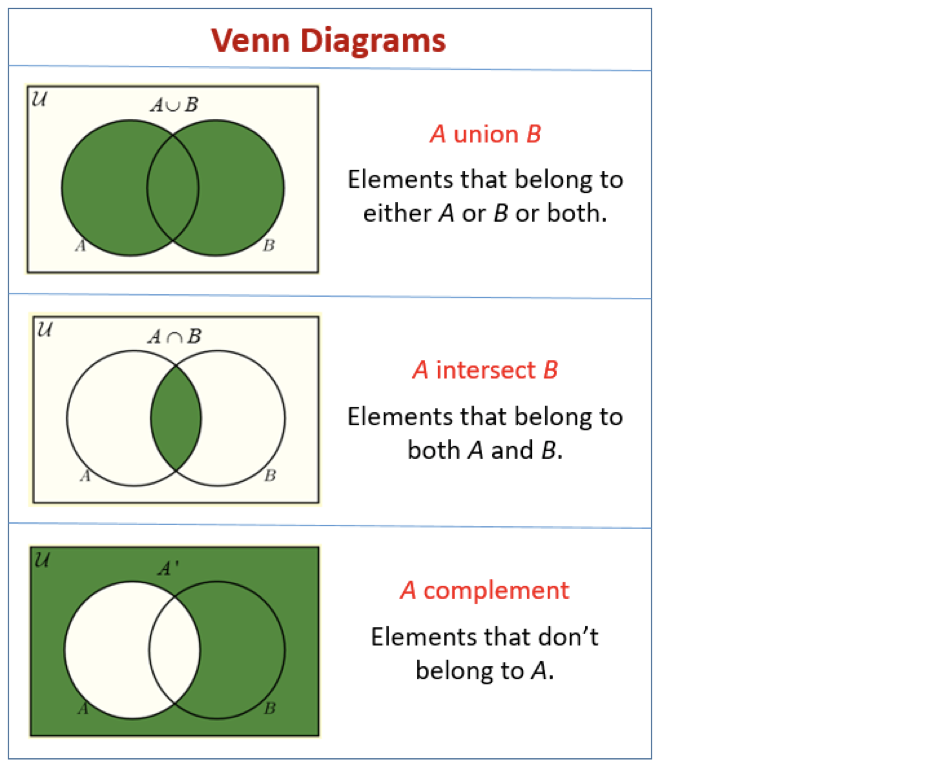
• Union of Sets:

  The union of two sets \(A\) and \(B\), denoted by \(A \cup B\), is the set of elements that are in \(A\), in \(B\), or in both. \[ A \cup B = \{x \mid x \in A \text{ or } x \in B\}. \]

• Intersection of Sets:

  The intersection of two sets \(A\) and \(B\), denoted by \(A \cap B\), is the set of elements that are in both \(A\) and \(B\). \[ A \cap B = \{x \mid x \in A \text{ and } x \in B\}. \]

• Complement of a Set:

  The complement of a set \(A\), denoted by \(A'\), is the set of elements not in \(A\) but in the universal set \(U\). \[ A' = \{x \in U \mid x \notin A\}. \]

• Universal Set:

  The universal set, denoted by \(U\), is the set that contains all elements under consideration in a particular context. All subsets are defined within this universal set.

• Cardinality of a Set:

  The cardinality of a set \(A\), denoted by \(|A|\), is the number of elements in the set.

• Venn Diagrams:

  Venn diagrams are visual representations of sets and their relationships, such as union, intersection, and complement.

Example 1: Union of Two Sets

Given \(A = \{1, 2, 3, 4\}\) and \(B = \{3, 4, 5, 6\}\), find \(A \cup B\).

Solution:

Step 1: Combine all unique elements of \(A\) and \(B\): \[ A \cup B = \{1, 2, 3, 4, 5, 6\}. \] Therefore, \(A \cup B = \{1, 2, 3, 4, 5, 6\}\).

Example 2: Intersection of Two Sets

Given \(A = \{1, 2, 3, 4\}\) and \(B = \{3, 4, 5, 6\}\), find \(A \cap B\).

Solution:

Step 1: Identify the common elements in \(A\) and \(B\): \[ A \cap B = \{3, 4\}. \] Therefore, \(A \cap B = \{3, 4\}\).

Example 3: Complement of a Set

Given \(U = \{1, 2, 3, 4, 5, 6, 7\}\) and \(A = \{2, 4, 6\}\), find \(A'\).

Solution:

Step 1: List all elements in \(U\) that are not in \(A\): \[ A' = \{1, 3, 5, 7\}. \] Therefore, \(A' = \{1, 3, 5, 7\}\).

Example 4: Cardinality of Sets and Venn Diagram Application

In a survey, 20 students like basketball, 15 like football, and 10 like both sports. How many students like at least one of the two sports?

Solution:

Step 1: Use the principle of inclusion-exclusion: \[ |A \cup B| = |A| + |B| - |A \cap B|. \] Step 2: Substitute the values: \[ |A \cup B| = 20 + 15 - 10 = 25. \] Therefore, 25 students like at least one of the two sports.