2.6 Quadratic Equations and Inequalities

Quadratic equations and inequalities involve a variable raised to the second power. They are fundamental in algebra and appear in various real-world applications.

Key Concepts:

• General Form of a Quadratic Equation:

  \[ ax^2 + bx + c = 0, \quad a \neq 0 \] where \(a\), \(b\), and \(c\) are constants.

• Quadratic Formula:

  Used to solve quadratic equations: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. \]

• Ways to Solve Quadratic Equations:

  • By factorization.
  • By completing the square.
  • By using the quadratic formula.

• Discriminant:

  The discriminant \(\Delta = b^2 - 4ac\) determines the nature of the roots:
  • If \(\Delta > 0\), there are two distinct real roots.
  • If \(\Delta = 0\), there is one real root (a repeated root).
  • If \(\Delta < 0\), there are no real roots (two complex roots).

• Graph of a Quadratic Function:

  The graph of \(y = ax^2 + bx + c\) is a parabola:
  • If \(a > 0\), the parabola opens upwards.
  • If \(a < 0\), the parabola opens downwards. \begin{figure}[h!] \centering
    
    \caption{Three cases for quadratic graph, depending on discriminant.} \label{fig:your-label} \end{figure}
  The vertex is given by: \[ x = -\frac{b}{2a}. \]

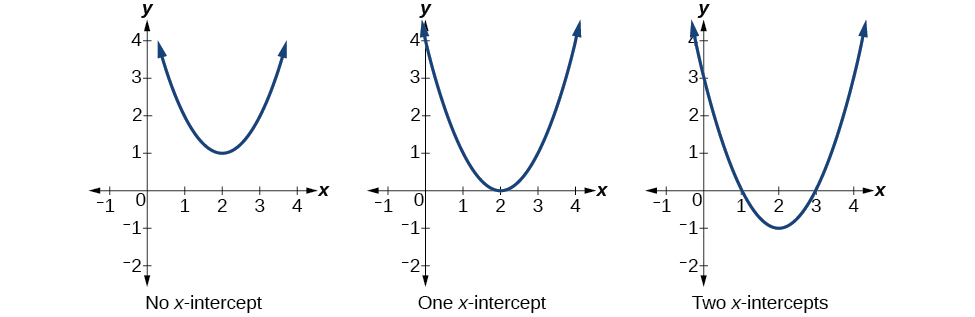
• Vieta's Formulas for Roots:

  • Sum of roots: \(r_1 + r_2 = -\frac{b}{a}\).
  • Product of roots: \(r_1 \cdot r_2 = \frac{c}{a}\).

• Constructing a Quadratic Equation from Given Roots:

  If the roots of a quadratic equation are \( \alpha \) and \( \beta \), then the equation can be formed using Vieta's formula: \[ x^2 - (\alpha + \beta)x + \alpha\beta = 0 \] This formula uses the sum and product of the roots to construct the quadratic equation. See Example 5.

Example 1: Solve \(x^2 - 5x + 6 = 0\) by factorization.

Solution:

Step 1: Factorize the quadratic equation: \[ x^2 - 5x + 6 = (x - 2)(x - 3). \] Step 2: Solve for \(x\): \[ x - 2 = 0 \implies x = 2, \quad x - 3 = 0 \implies x = 3. \] Therefore, the solutions are \(x = 2\) and \(x = 3\).

Example 2: Solve \(x^2 + 6x + 5 = 0\) by completing the square.

Solution:

Step 1: Rewrite the equation: \[ x^2 + 6x = -5. \] Step 2: Complete the square: \[ x^2 + 6x + 9 = -5 + 9 \implies (x + 3)^2 = 4. \] Step 3: Solve for \(x\): \[ x + 3 = \pm \sqrt{4} \implies x + 3 = 2 \quad \text{or} \quad x + 3 = -2. \] Step 4: Simplify: \[ x = -1 \quad \text{or} \quad x = -5. \] Therefore, the solutions are \(x = -1\) and \(x = -5\).

Example 3: Solve \(2x^2 - 3x + 1 = 0\) using the quadratic formula.

Solution:

Identify the coefficients: \[ a = 2, \quad b = -3, \quad c = 1. \] Use the quadratic formula: \[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(2)(1)}}{2(2)}. \] Simplify: \[ x = \frac{3 \pm \sqrt{9 - 8}}{4} = \frac{3 \pm 1}{4}. \] Solve for \(x\): \[ x = \frac{3 + 1}{4} = 1 \quad \text{or} \quad x = \frac{3 - 1}{4} = \frac{1}{2}. \] Therefore, the solutions are \(x = 1\) and \(x = \frac{1}{2}\).

Example 4: Find the nature of the roots for \(x^2 + 4x + 5 = 0\).

Solution:

Step 1: Calculate the discriminant: \[ \Delta = b^2 - 4ac = 4^2 - 4(1)(5) = 16 - 20 = -4. \] Step 2: Interpret the result: \[ \Delta < 0 \implies \text{the equation has two complex roots.} \] Therefore, the roots are complex.

Example 5: Write a quadratic equation whose roots are \(-\frac{1}{2}\) and \(3\).

Solution:

Step 1: Use Vieta's formulas for roots: \[ \text{Sum of roots: } r_1 + r_2 = -\frac{b}{a}. \] \[ \text{Product of roots: } r_1 \cdot r_2 = \frac{c}{a}. \] Step 2: Substitute the given roots \(r_1 = -\frac{1}{2}\) and \(r_2 = 3\): \[ \text{Sum of roots: } -\frac{1}{2} + 3 = \frac{5}{2}. \] \[ \text{Product of roots: } \left(-\frac{1}{2}\right)(3) = -\frac{3}{2}. \] Step 3: Write the quadratic equation using the general form: \[ a \cdot x^2 - (\text{sum of roots}) \cdot x + (\text{product of roots}) = 0. \] Substitute the values and assuming a=1 for the simplest case: \[ x^2 - \frac{5}{2}x - \frac{3}{2} = 0. \] Step 4: Eliminate fractions by multiplying through by 2: \[ 2x^2 - 5x - 3 = 0. \] Therefore, the quadratic equation is \(2x^2 - 5x - 3 = 0\).